
|
|

|
|
Flat Universe |
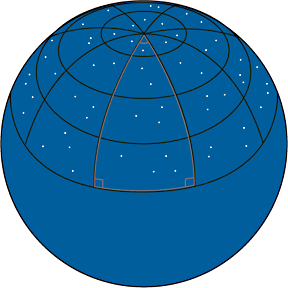
Positive Curvature Universe |
Negative Curvature Universe |
What is the shape of the Universe? An interesting question, for sure, and one that carries with it other implications - like what the ultimate fate of the Universe will be. For many years, scientists have proposed that there are three possibilities for the curvature (or shape) of the Universe. The Universe can be flat, like a piece of paper. Or it can have a positive curvature, like a sphere. Or it can have a negative curvature, like the middle part of a horse's saddle. To a certain degree, the curvature the Universe has depends on how much mass there is in the Universe...and the amount of mass will determine its ultimate fate. So, it is of more than just a passing fancy that we might want to measure the curvature of the Universe. But how exactly do you do that?
In this lesson, we will explore one possible way to measure the curvature of the Universe, namely, by measuring the sum of the angles in a triangle in the Universe. Depending on the shape of the Universe, the sum will be either less than, equal to, or greater than 180 degrees. Of course, we can't measure just ANY triangle...we have to use a very big triangle in order to be able to discern the shape of the Universe. Every triangle will give the result of 180 degrees if you measure just a teeny tiny part of a very big space...no matter what its curvature is.

|

|

|
|
Flat Universe |
Positive Curvature Universe |
Negative Curvature Universe |
So how do you measure a very big triangle in the Universe? That will be discussed as well, since it is something that NASA's Microwave Anisotrophy Probe (MAP) mission will do in the next few years. But first, let's learn about different shapes, or geometries, and how they effect the sums of the angles of a triangle. This standards-based topic, called Non-Euclidean Geometry, will challenge your brain - but only because you are used to the flat space and rules of Euclidean Geometry. So be prepared for a mind-bending exercise!
When most students study geometry, they learn Euclidean Geometry - which is essentially the geometry of a flat space. Euclidean Geometry is based upon a set of postulates, or self-evident proofs. Such proofs present "on obvious truth that cannot be derived from other postulates." Here are Euclid's postulates:
The fifth postulate is known as the Parallel Postulate. This Postulate was rewritten by Scottish scientist and mathematician John Playfair (1748-1819) as the following (referred to as the Playfair axiom): "Through a given point not on a given line, there passes at most one line that is parallel to the given line."
It was the obvious difference between the first 4 postulates and the fifth which led mathematicians to believe that in fact the fifth was not a postulate, but could be deduced from the first 4. In trying to do so, they discovered elliptic geometry and hyperbolic geometry!
If you assume the fifth postulate is false, there are 2 possible negations:
The first assumption was investigated by German mathematician Carl Friedrich Gauss (1777-1855), Russian mathematician Nikolai Lobachevsky (1792-1856), and Hungarian mathematician Janos Bolyai (1802-1860). They discovered that it led to a new geometry that did not contradict any of the other postulates. If they replaced the Parallel Postulate with this new assumption, they had discovered the non-Euclidean geometry called hyperbolic geometry.
German mathematician Georg Friedrich Bernhard Riemann (1826-1866) investigated the second assumption. If the Parallel Postulate is replaced with this postulate, again none of the other postulates were violated. The non-Euclidean Geometry this set of postulates creates is called elliptic geometry.
All of the theorems in Euclidean Geometry which do not rely on the Parallel Postulate apply intact in the non-Euclidean geometries. One theorem, perhaps the most famous example, which does rely on the Parallel Postulate is the Triangle Sum Theorem, which states: the sum of the three angles in a triangle is 180°. Since students are probably already familiar with the flat space of Euclidean Geometry and how the angles of a triangle in that space add up to be 180°, we will focus on seeing what triangles look like and behave like in elliptic and hyperbolic spaces.
Elliptic Geometry
 |
You can use the surface of a sphere as a model for elliptic geometry. But if you do, you must change the wording of the Euclidean Postulates slightly. In elliptic geometry, the word "line" is replaced by "great circle". A great circle is defined as any circle on the surface of a sphere for which the diameter passes through the center of the sphere. You also need to define "pole points" to be points on the opposite ends of any diameter of the sphere. To create elliptic geometry, Riemann assumed that through a given point not on a line, there passes no lines parallel to that given line. This new geometry introduces a few changes. In Euclidean geometry, lines are infinite in length. In elliptic geometry, great circles never end, but they are finite in length. A line segment is now defined as an arc of a great circle, or the distance along the great circle between two points. When a straight line is extended, its ends eventually meet forming a great circle. Any two "straight lines" eventually meet, since any two great circles intersect at pole points. One result of this change in the Parallel Postulate is that the Triangle Sum Theorem has a different ending: The sum of the three angles in a triangle in elliptic geometry is always greater than 180°. |
Hyperbolic Geometry
 |
To find a model for a hyperbolic geometry, we need one in which for every line and a point not on that line, there is more than one parallel line. French mathematician Henri Poincaré (1854-1912) came up with such a model, called the Poincaré disk. The Poincaré disk consists of all the points on the interior of a circle. Lines in this geometry are arcs inside the circle, but not just any arcs. The arcs must have their ends on the circumference of the circle and must be perpendicular to the circle at both end points. As you may have guessed, this geometry also changes the ending of the Triangle Sum Theorem so that it reads: The sum of the three angles of a triangle in this geometry is always less than 180°. |
Materials:
Directions:
For a more complete discussion of Euclidean and Non-Euclidean Geometries and reasons to teach Non-Euclidean Geometries in your classroom please visit http://math.rice.edu/~joel/NonEuclid/NonEuclid.html.This website also contains a web-based program, which your students can use to investigate a Poincaré Disk.
Origin and Evolution of the Universe: In grades 9 -12 all students should understand that:
"Early in the history of the universe, matter, primarily in the form of hydrogen and helium, clumped together by gravitational attraction to form countless trillions of stars. Billions of galaxies, each of which is a gravitationally bound cluster of billions of stars, now form most of the visible mass of the universe; Stars produce energy from nuclear reactions, primarily the fusion of hydrogen to form helium. These and other processes in stars have led to the formation of all the other elements."
Nature of Scientific Knowledge