Dark Matter: Probing What You Can't See

Astronomers have known for many years that most of the matter in the Universe is invisible. Identifying this "dark matter" is a crucial step in understanding of the Universe. Dark matter is transparent and emits no light. Different theories for the composition of dark matter predict the scales on which it can clump gravitationally. The gravitational attraction of the dark matter drives the development of structure in the Universe. But if we can't see it, how will we ever learn anything about it? How will we ever answer such questions as

• What is dark matter?

• Is there more than one type of dark matter?

• What roles did dark matter play in the formation of structure in the Universe?

• Are there other relics from the early Universe awaiting our discovery?

• Does the dark matter content change as we look back in time?

Astronomers are coming up with all sorts of inventive ways to approach the unveiling of dark matter. We'll learn more about this research in later sections, as this lesson looks into how we learn about things we cannot see...by using standards-based subjects such as gravity, rotation, torque, equilibrium of forces, and more.

Student Labsheets

• Dark Matter Activity Labsheet

Pre-Requisites

• General understanding of the development of the universe and an introduction to the idea of dark matter. See Imagine the Universe! for resources and background information on these topics.

• Previous introduction to the concept of force and turning effect (torque). Students will apply these concepts in this lesson's lab.

Background Information

Evidence for Dark Matter

• In 1930, Fritz Zwicky discovered that the galaxies in the Coma cluster were moving too fast to remain bound in the cluster according to the Virial Theorem. The Coma cluster is about 300 million light-years away.

  Optical Image of Coma Cluster of Galaxies

   

  The Virial Theorem states that stable galaxies should obey U = -2K, where U is the potential energy and is equal to -aGMm/r (a is between 0.5 - 2, depending on the mass distribution), and K is the kinetic energy and is equal to 0.5 mv². In other words, stable galaxies should obey M = v²r/aG. We can measure M, r, and v from observations of the galaxies. We can use our measured values of M and r to calculate V. When you compare the two values of V, we see that V_measured > V_calculated, which implies M is too small.

• Additional evidence is the shape seen in galaxy rotation curves. If you measure the velocity of stars and gas clouds at various distances from the centers of their galaxies (by using their Doppler shifts), and plot the results, you see that the velocities flatten out. Since v² = GM/r (where the mass M is inside the radius r), then if V flattens out, M must increase with increasing r.

• Adding the amount of light emitting matter in the galaxies in clusters to the amount of hot gas between the galaxies in the cluster (3-5 times more than the mass in the stars) still leads us without enough mass to hold the cluster together. To hold in the hot gas, you need 5-10 times more mass than what you see.

Superposed on an optical picture of a group of galaxies is an image taken in X-ray light. This picture, taken by ROSAT, shows confined hot gas highlighted in false purple color, and provides clear evidence that the gravity exerted in groups of galaxies exceeds all the individual component galaxies combined. The extra gravity is attributed to dark matter. Credit: Richard Mushotzky

 

• The rotating disks of the spiral galaxies we see are not stable. Dark matter halos provide the gravitational force to hold the galaxies together. They also maintain the rapid velocities measured in the outermost stars of the galaxies.

Possibilities for Dark Matter: What in the Universe could it be?

There are two basic possibilities for what sort of matter may make up the "missing mass". First, it may be regular matter that is just not hot enough to be emitting any radiation. Alternatively, it might be some sort of more exotic matter -- the likes of which we don't have naturally here on Earth (but may one day be able to create in our particle physics laboratories). So far, all we seem to know about the matter that makes up most of the Universe is that it behaves just like regular matter as far as gravity is concerned.

More Details About the Possibilities for Dark Matter

The matter that comprises dark matter might be baryonic, non-baryonic -- or perhaps a combination of the two. Below we give details about what each type of matter means, and what the possibilities are for its being the solution to the dark matter mystery.

• Baryonic: Baryonic matter is ordinary matter; what would make it dark is if it is just not hot enough to be emitting any radiation. MACHOs, dwarf stars of all colors, black holes, neutron stars, gas, and dust would all be possibilities.

  Normal matter in the Universe is 75% hydrogen and 25% helium. As the Universe cooled from the Big Bang, there were 7 times as many protons as neutrons available to form matter. Almost all of the deuterium which formed made helium. The relative amounts of hydrogen, deuterium, and helium depend on a factor called eta, where eta = (protons + neutrons)/photons. Eta is very small. We measure about 1 or 2 atoms per 10 cubic meters of space versus over 400 photons per cubic centimeter. The measured value for eta is the same or a little smaller than that derived from comparing relative amounts of hydrogen, deuterium, and helium. So while we may be missing a little bit of baryonic matter, we are not missing enough to account for the observed effects of dark matter.

  MACHOs are "MAssive Compact Halo Objects". Some have been discovered (through gravitational microlensing). Not enough have been found, however, to account for the dark matter effects in galaxies.

  The creation of tiny black holes, called primordial black holes, in the very young Universe might also lead to a great deal of invisible mass. There cannot be too many primordial black holes, or we would see their effects on stars circulating in the outer regions of our Galaxy.

• Non-Baryonic: Non-baryonic matter consists of exotic forms of matter such as neutrinos, WIMPs, axions, supersymmetric particles.

  Neutrinos are believed to have zero mass and travel at the speed of light. There are 100 million neutrinos per cubic meter. They come in 3 types - electron, muon, and tau. There cannot be more types because that would lead to more primordial helium than we see. We don't seem to see enough neutrinos from the nuclear reactions in the Sun. If they oscillate between different types, then this problem is solved. However, if the oscillate, they must have some amount of mass and could account for the "hidden mass" in the Universe. This problem is an area of much current research.

  Axions are hypothetical particles which would have typical masses around 10^-6 eV/c². There would be 10⁸ per cubic centimeter and their velocities would be very low. We would be able to detect them when they convert to low energy photons after passing through a strong magnetic field.

  WIMPs, or "Weakly Interacting Massive Particles", are hypothetical particles predicted by supersymmetry theories in particle physics. Supersymmetry tries to unify the four forces of physics by adding extra dimensions to space. WIMPs would have easily been detected in accelerators if their masses were less than 15 GeV/c². The lightest WIMPS would be stable and could still exist in the Universe, comprising most (if not all) of the dark matter.

Revealing the Nature of Dark Matter

Scientists at Bell Laboratories are studying images of faraway galaxies that are "lensed" by intervening concentrations of mass. As the light from a distant galaxy passes by a large mass concentration, its ray path is bent, causing the distant source to appear at an altered place on the sky and resulting in a tell-tale distortion of its shape. This gravitational lensing effect provides the first, and currently only, way to directly "weigh" cosmic mass. Clusters of galaxies contain a considerable amount of dark matter (at least five times as much mass as you can see in the galaxies and the hot gas between them) and make excellent, although complicated lenses. By studying the images that are created by gravitational lensing, scientists are able to determine the mass and location of the dark matter in the cluster.

An Introduction to Moment of Force

One of the fundamental beliefs about Dark Matter is that it behaves like ordinary matter when it comes to gravity. Remember that Newton taught us that gravitational force is defined by the equation:

where F is gravitational force between two objects, G is the universal gravitational constant, M₁ and M₂ are the masses of two objects, and R is the distance between these two objects. In other words, Dark Matter exerts gravitational force on the masses around it. What Newton's Law doesn't say (and what Einstein showed) is that the gravitational force also affects light. Scientists study the effects due to this force to determine how much dark matter there is, and where it is located.

In physics, a common introductory-level subject is forces and how they act on bodies. The effect produced on a body by a force of a given strength and direction depends on the position of the line of action of the force relative to the position of a reference point on the body . So, you have to know how strong the force is and where it is located. The force arm, or moment arm, of a force can be found by giving the perpendicular distance between some reference point (usually an axis of the object, such as a rotation axis) and the line of action. The mathematical product of the force and the force arm is called the moment of force, or the torque, about the axis.

Look at the situation shown in the image below. The force F₁ wants to cause the object to rotate in a counterclockwise direction; F₂ wants the object to rotate in a clockwise direction. Since these forces act in opposite directions relative to the reference point, they have opposite signs. For the object not to rotate at all, the torque (or turning effect) caused by one force must be exactly equal to the torque caused by the other force. In other words, the sum of all of the torques applied to an object must be equal to zero.

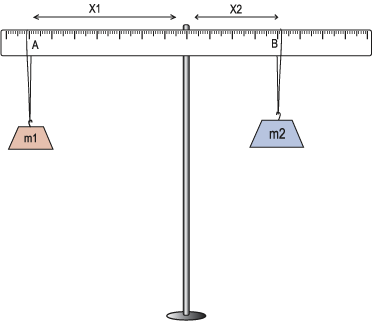
In the case shown above, F₁ is equal to the mass of the object put at location A times the acceleration due to gravity. So, F1 = m₁ * g, where g on Earth is equal to 9.8 m/sec². Similarly, F₂ is equal to the mass of the object put at location B times the acceleration due to gravity, m₂*g . The torque introduced by each force is then F₁*X₁ and F₂ * X₂, where X₁ and X₂ are the distances measured from points A and B to the reference point (in this case, the suspension point, O). For the meter stick to be in balance, F₁*X₁ must be equal in value to F₂*X₂. Solving this equation, we see that for equilibrium, M₁X₁ = M₂X₂. Think about what this means: a smaller mass placed farther from the axis will balance a larger mass placed nearer the axis. Try this the next time you get into a revolving door. You have to push much less if you push toward the outside of the door than if you push near the inside!

Teacher Notes

• Find the Missing Mass Activity

  You must prepare your "hidden masses" before doing the lab. You'll need:

  • Paper plates (the really cheap ones work fine)
  • Masses (at least 7 per plate; quarters work great)
  • Tape or glue
  • Ruler or measuring tape

   

  Take a paper plate and carefully use measurements to find the center of the plate. Punch a small hole at the center location. We used a small Phillips screwdriver, which we could then also use as the support for our "balance". Draw a diameter through this center all the way to the edges.

   

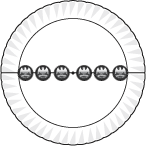
  On one radius, place three quarters along the line and trace them on the paper plate. On the other side, create traces at the exact same distances as you put the quarters on the first side. This will create six outlines of quarters with the three on one side being at the exact same distances from t he center as the three on the other.

   

  You are now ready to tape or glue quarters into place in these image locations. You should use 7 quarters. Put one quarter in each of the six locations and then decide at which location to put the remaining quarter. If you make a classroom set of these hidden mass plates, consider putting the extra quarter at different locations for various plates. Now tape a second paper plate on top of this plate, so that they are in the "stacked" on top of one another. Tape or glue this plate into place.

   

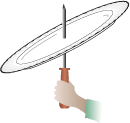
  Insert the screwdriver into the hole in the center of the bottom plate and punch through the top plate. You will notice that the plate does not balance on the screwdriver, but tilts distinctly to the side with the extra quarter on it. You now have your hidden mass plate ready for use.

   

• Extension 1: Taking the Lab to a Higher Level

  You can make this activity more difficult by using two extra masses. Put one extra mass on each side, but in a different location relative to the center point. When the students do the lab, they will have to first determine the extra mass on the side that initially tilts down, then add an extra mass to the up side at this location to balance that mass and then balance the extra mass on the side that was initially up but will now be down. This version of the activity requires a deeper understanding of the concept of a turning effect (or a torque) and the mathematics behind it.

• Extension 2: Focus on Mathematics

  Scientists know that there is "dark matter" in the Universe; matter that we have not been able to see from Earth. Science experts are testing many scientific models for just what makes up this matter and how its presence effects the evolution of the Universe. Many models must be tested, and a sure definition has yet to be defined for dark matter.

  In math classes everywhere, the same type of investigations are occurring.

  Explorations like these are what is called "mathematical modeling" or may be coined "Dark Mathematics". This lesson is intended to get students to take data and determine the mathematical relationship behind them.

  Take me to the Dark Math Lesson

  The solution to the problem is that the x-value is an area of a square and the corresponding y-value is the side length of that square.

Additional Resources

• www.astro.queensu.ca/~dursi/dm-tutorial/cluster-sim.html

• www.astro.queensu.ca/~dursi/dm-tutorial/rot-vel.html

National Standards

Science

Origin and Evolution of the Universe: In grades 9 - 12 all students should:

"Early in the history of the universe, matter, primarily in the form of hydrogen and helium, clumped together by gravitational attraction to form countless trillions of stars. Billions of galaxies, each of which is a gravitationally bound cluster of billions of stars, now form most of the visible mass of the universe; Stars produce energy from nuclear reactions, primarily the fusion of hydrogen to form helium. These and other processes in stars have led to the formation of all the other elements."

Mathematics

Algebra: In grades 9 - 12 all students should:

• Represent and analyze mathematical situations and structures using algebraic symbols
• understand the meaning of equivalent forms of expressions, equations, inequalities, and relations
• judge the meaning, utility, and reasonableness of the results of mathematical manipulations
• Use mathematical models to represent and understand quantitative relationships
• identify quantitative relationships in a situation and determine the class or classes of functions that might model the relationships
• use symbolic expressions to represent relationships arising from various contexts
• draw reasonable conclusions about a situation being modeled