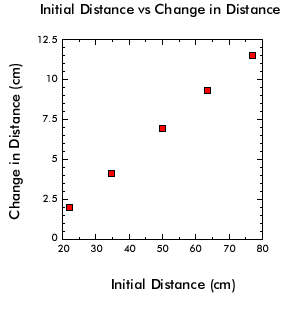
|
Galaxy # |
Initial Distance (cm) |
Final Distance (cm) |
Change in Distance (cm) |
|
1 |
22.0 |
24.0 |
2.0 |
|
2 |
34.6 |
38.7 |
4.1 |
|
3 |
49.9 |
56.8 |
6.9 |
|
4 |
63.5 |
72.8 |
9.3 |
|
5 |
77 |
88.5 |
11.5 |
We believe our Universe is expanding in size. This concept may seem familiar and commonplace now, but try to imagine what it was like in 1929 when Edwin Hubble first published his data and came to this conclusion. Our Universe was expanding, literally and figuratively.
If your math class needs a fresh way to for students to explore linear relationships or if your science class needs to develop an understanding of the expanding Universe, then this lesson is for you. The lesson consists of 3 Labs, only 2 of which are required. Lab C is an enrichment for higher level classes.
Lab A will ask students to take distance measures of sequins on elastic and plot the measures. From these plots, students will discover a linear relationship that will lead to the conclusion that "the further away you are, the further you travel when stretched."
Lab B will have students take the activity in the first lab one step further. Students will measure the velocity of each sequin and plot it (just as Hubble did with galaxies more than 70 years ago). Students will take time and distance measures to calculate the velocity. This provides a nice extension to Lab A, and demonstrates a connection to other subjects (i.e., astronomy).
For higher level students, Lab C can be substituted for Lab B, or done in addition to it. It is based on the fact that the relationship investigated here is not based on absolute values, but one that is concerned with the relative movement of the sequins. Absolute time is not important, only that we measure the locations of the sequins at different times (albeit the same times) for all of the sequins. In other words, "snapshots" in time work just fine and no measurement of time is needed. If your students perform all 3 Labs, have them compare and discuss the 3 results.
If you look at the data Hubble (1929), and 2 years later, Hubble and Humason (1931), published, you were led to the following inevitable conclusion: the further away from us you were, the faster away from us you were moving. While this may seem to be an odd thing, it is a consequence of the expansion of space. In this lesson, we will explore this concept; you will discover for yourself that when space expands, the further away you are, the faster away you move.
In the 1920s, American astronomer Edwin Hubble changed the way we thought of our Universe. First, he showed us that the fuzzy patches of light seen through the telescope were in fact other galaxies, far outside of our own Milky Way. Then, he spread the light of those galaxies into a spectrum. From this, he could see what each was made of and how fast it was moving. The latter was determined by the red shift, or Doppler Shift. You can read about the Doppler Shift in the next section. He could then plot on a graph velocity versus the distance for each galaxy he measured. He had determined the distance by the apparent brightness of the galaxy. When he made his plot, he found that the galaxies seemed to lay on a straight line -- in other words, their velocities were proportional to their distances! This discovery led to what is now called Hubble's Law. This rate of expansion is called Hubble's constant (Ho). It is written as
v = Ho * d
Based on these observations, an amazing conclusion was reached by Edwin Hubble and his colleagues: our Universe was expanding.
Important Note: Most galaxies are moving away from us. Not all, but most. Our nearest spiral neighbor, Andromeda, is in fact moving toward us and will one day collide with our Milky Way. Andromeda is moving toward us for the same reason galaxies themselves are not expanding -- gravity. It is important to distinguish this. Space itself is expanding, not the sizes of objects in the space. Gravity stops them from getting any larger than they are.
When you spread out the light from a stationary galaxy, you see dark lines (called spectral lines) at particular wavelengths due to the elements in that galaxy. This fact, coupled with the existence of the Doppler Shift due to the movement of sources of waves, provides us with an important tool in understanding the expansion of the Universe. Specifically,
If each 1 cm of elastic stretches to be 1.5 cm in length, then an object 1 cm away will move to 1.5 cm away. However, an object 10 cm away will move to 15 cm -- a full 5 cm from where it started. This is because each cm of the 10 cm will increase by 0.5 cm, leading to a cumulative total change of 5 cm. So an object 100 cm away will move to 150 cm! In other words, the farther away you were to start with, the farther away you move with each stretch. Thanks to the linear expansion of the elastic.
This is an analogy to what is happening in the Universe. The galaxies aren't moving, but they appear to be moving away from us because the space between us and them is expanding. And we now understand that the farther away you started, the more away you move with each expansion. Since space continually expands, the expansion is a function of time, and we measure your movement away from us by your velocity. The result is that since space is expanding, the farther away you are, the faster away you move!
|
Galaxy # |
Initial Distance (cm) |
Final Distance (cm) |
Change in Distance (cm) |
|
1 |
22.0 |
24.0 |
2.0 |
|
2 |
34.6 |
38.7 |
4.1 |
|
3 |
49.9 |
56.8 |
6.9 |
|
4 |
63.5 |
72.8 |
9.3 |
|
5 |
77 |
88.5 |
11.5 |

Origin and Evolution of the Universe: In grades 9 - 12 all students should:
"Early in the history of the universe, matter, primarily in the form of hydrogen and helium, clumped together by gravitational attraction to form countless trillions of stars. Billions of galaxies, each of which is a gravitationally bound cluster of billions of stars, now form most of the visible mass of the universe; Stars produce energy from nuclear reactions, primarily the fusion of hydrogen to form helium. These and other processes in stars have led to the formation of all the other elements."
Algebra: In grades 9 - 12 all students should:
Measurement: In grades 9 - 12 all students should: