Looking Out Is Looking Back...

in a VERY Big Place

Objectives

In this lesson, we will explore the size of our Universe by understanding how long it takes to travel around from object to object in it - even if you travel at the speed of light! In making our exploration, we will examine ways of measuring distance, make inferences regarding space travel, identify the distance relationship between Earth and other objects in the Universe, develop formulas and procedures for determining measurements to solve problems, and choose and use the appropriate units for our problems. Whew! We will also create a timeline of historical events... possibly all the way back to a time when the Earth did not yet exist!

Student Worksheets

• Warm-Up Worksheet
• Part I Worksheet
• Part II Worksheet

Teacher Notes & Answers

Students often have difficulty comprehending just how enormous the Universe actually is. In an effort to help them grasp this abstract concept, this lesson develops a path along which they encounter increasingly larger numbers. This script allows them to correlate distance to the more tangible concept of time. If you tell a student a planet is 10,000,000,000 kilometers away, it doesn't mean as much as when you tell them it would take a car traveling at 100 km/hr 100,000,000 hours to make the journey. This point is emphasized when students realize that is 4,166,667 days or 11,415.5 years!

To introduce the lesson, have the students measure the diameter of an M&M candy. Then have them calculate distances to familiar places in terms of the numbers of M&Ms required to cover the distances. This activity will allow them to start associating a familiar size to distances, and to begin thinking in terms of big numbers. The next part of the lesson will be where the students manipulate the actual numbers involved in exploring the Universe.

The diameter of an M&M is 1 cm. So, if you to want to lay them end to end and cover the following distances, you will need the stated number of candies.

The questions/problems can be posed to students to take them to the ever larger numbers encountered in our Universe.

1.) What if those relatives lived 400,000 km away on the Moon; how long would it take to get to their house if you traveled by car at 100 km/hr? 4000 hrs.

2.) If you travel at 100 km/hr, just how long would it take you to reach our most distant planet? 60,000,000 hrs.

How many years would it take you to reach Pluto? 6849.3 years

3.) A jet travels at 1000 km/hr. At this faster speed, what is our travel time to Pluto? 6,000,000 hrs.

How many years will it take us? 684.9 years

Before continuing, draw student's attention to the definition of a light-year. If you were traveling at the speed of light, a light year would be the distance that you would travel in one year. You might even show them how it is "derived" from the speed of light. Specifically, light travels at 300,000 km/sec, therefore

Distance traveled in 1 year = (distance traveled in 1 s); (60 sec/min); (60 min/hr); (24 hr/day) ; (365 days/yr.) = 9.4608 x 10¹² km

4.) The star outside of our solar system that is closest to Earth is Alpha Centauri C, also called Alpha Proxima. It is 40,000,000,000,000 (40 trillion) km away. How many light years is that? 4.21 light-years

If we hoped aboard our jet, how long would it take us to get to Alpha Centauri C?

40,000,000,000 hours

How many years would that take? 4,566,210.0 years

5.) First convert 600 light-years into kilometers. 5.7 x 10¹⁵ km Traveling at 1000 km/hr. by jet, how long would it take to reach Betelgeuse? 5,700,000,000,000 hrs.

How many years is that? 650,684,931.5 years

Suggested Extension to Part I: For extra practice working with large distances, have the students go to The Facts page of each planet in the Solar System section of StarChild. There they will find the distance of each planet from the Sun. Have the students calculate the time it would take to travel to each planet by car (100 km/hr.) or by jet (1000 km/hr). For a real challenge, have the students calculate travel time using the speed of the Space Shuttle (27,200 km/hr.) at main engine cut-off which occurs 112 km above Earth's surface.

The amount of time it takes for light to travel from the objects listed below to Earth is shown.

• You will have students imagine that they are beings from each of the astronomical objects on their list (see materials). Tell them to imagine that they can look towards the Earth and observe what is happening. Due to the distance between the Earth and these objects, these beings will view the Earth as it was some time in the past, depending upon the distance light has to travel from the Earth to reach them.

• The students research what the cosmic beings are seeing, with perspective to the Light Distance they are away on the Earth. For example, a being on Mars would be viewing what happened in the classroom 4 minutes ago. If you choose observers on Pluto, they will see what happened 5.4 years ago.

• The students display the information that they researched on a timeline marking the time scale in years and distances (in kilometers) from Earth.

• Your students will be able to find many cosmic objects, at all sorts of distances, between a few light-minutes and billions of light-years. They will be able to find events in the history of Earth between about 4.5 billion years ago and the present. For example,

• The oldest mineral is dated at 4.2 billion years --zircons from western Australia
• The Jurassic Period-- 208 to 146 Million Years Ago
• Saint Joan of Arc, Patron Saint of France -- born 01/06/1412; died 05/30/1431.

• For objects that are further away than 4.5 billion light-years, the Earth will not make a viable reference point ...since it will not yet have formed! It is an amazing concept to grasp that we are receiving light from distant sources which left those sources and began travelling here before the Earth (or any part of our solar system) even existed! For objects further away than 4.5 billion light-years, have the students brainstorm about how they might then reference time and distance.

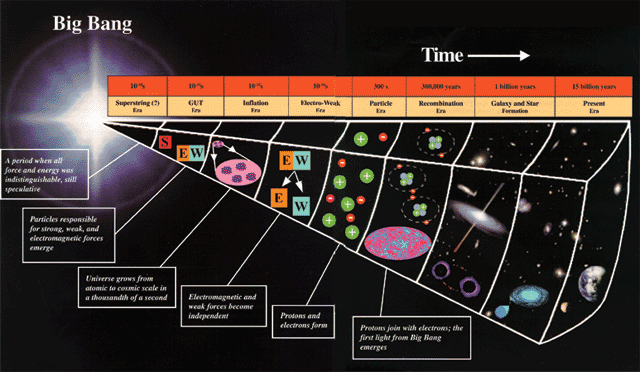
Here is a timeline of the "History of the Universe" that you might want to share with your students. For a full-scale version, select the link below and print it in LANDSCAPE mode.

History of the Universe

Additional Resources

• "Powers of Ten" video. It can usually be found in the Astronomical Society of the Pacific's catalog for about $40. Sometimes you can find it on sale! See https://www.mailordercentral.com/aspsky/.

• Universe at Your Fingertips - A collection of 90 of the best classroom-tested, hands on activities, collected from a variety of sources, some published before, others not. Designed for grades 4 - 9, but can be extended to grades 3 - college. Usually about $35. See https://www.mailordercentral.com/aspsky/.

Relevant National Standards

• The Origin and Evolution of the Universe

• Historical Perspectives on the History and Nature of Science

• develop a deeper understanding of very large and very small numbers and of various representations of them;

• make decisions about units and scales that are appropriate for problem situations involving measurement;

• use unit analysis to check measurement computations.

• Social studies programs should include experiences that provide for the study of the ways human beings view themselves in and over time.

• Social studies programs should include experiences that provide for the study of relationships among science, technology, and society.